Fig 1. Recursive Version
Abstract: A certain kind of problems can be described with recursive procedures quite efficiently. But sometime you need strict control over recursive procedures which produces a huge amount of data, which adds difficulty to coding. Python generators, which are available in Python 2.2 or later, allows us to control these procedures easily preserving concise programs.
The source code mentioned in this document is here. The plain text version is here.
No one doubts the power of recursion. Although it sometime might look a little bit complicated, it normally provides a quick way to describe a solution. This is especially true if the size of data handled by a procedure grows exponentially. Traversing a tree is a good example. Since each node in a tree has one or more nodes, as the procedure goes down the tree, the number of nodes grows in exponential order. But if all nodes are homogeneous, the same procedure can apply to every node again and again.
Tree traversal is a trivial example of recursion, because almost every Computer Science textbook explains this. Probably everyone will happily choose recursion for tree traversal without any deep consideration. Of course however, there are many tasks where recursion works pretty well. So let us take another example.
Consider the following function f which takes a set of vectors (V1, V2, V3, ... , Vn) and returns a set of all possible combinations of each element of Vi. Each combination consists of n-element vectors (xi1, xi2, ... , xim) where xij is an element of Vi. The total number of vectors this function returns is |V1| x |V2| x |V3| x ... x |Vn|.
Let us consider implementing this function in Python. For simplicity, we use String objects to represent each vector Vi. The function returns a set of vectors as a list. The expected result is the following:
f([]) --> [''] # 1
f(['abc']) --> ['a', 'b', 'c'] # 3
f(['abc', 'xyz']) --> ['ax', 'ay', 'az', 'bx', 'by', 'bz', 'cx', 'cy', 'cz'] # 9
f(['abc', 'xyz', '123']) --> ['ax1', 'ax2', 'ax3', 'ay1', 'ay2', 'ay3', 'az1', 'az2', 'az3',
'bx1', 'bx2', 'bx3', 'by1', 'by2', 'by3', 'bz1', 'bz2', 'bz3',
'cx1', 'cx2', 'cx3', 'cy1', 'cy2', 'cy3', 'cz1', 'cz2', 'cz3'] # 27
At a first glance, it looks easy to implement. You might think that this function can be written easily without using any recursion. Let's try.
First, if you don't want to use recursion at all, your program might end up with something like this:
def f0(args): counter = [ 0 for i in args ] r = [] while 1: r.append("".join([ arg1[i] for arg1,i in zip(args, counter) ])) carry = 1 x = range(len(args)) x.reverse() # x == [len(args)-1, len(args)-2, ..., 1, 0] for i in x: counter[i] += 1 if counter[i] < len(args[i]): carry = 0 break # leave "for" counter[i] = 0 else: break # leave "while" return r
Without using recursion, you have to remember intermediate
states somehow to produce all possible solutions. In this program,
I tried to emulate something like full-adders. First the program
prepares a list of integers and then repeatedly attempts to add
one to the least significant digit. At each iteration, it
concatenates elements in each argument and put it into variable
r. But the behavior of this program is not so
clear, even though some variable names such as
"carry" are suggestive.
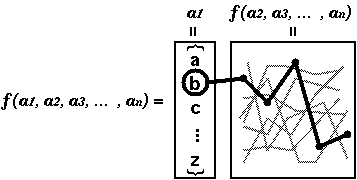
Now you have recursion. The function f can be defined recursively as follows:
| f(Vi, Vi+1, ... , Vn) = | ({xi1} + f(Vi+1, ... , Vn)) + |
| ({xi2} + f(Vi+1, ... , Vn)) + | |
| ... | |
| ({xim} + f(Vi+1, ... , Vn)) . |
With this definition, you can make the program a much simpler by calling itself:
def fr(args): if not args: return [""] r = [] for i in args[0]: for tmp in fr(args[1:]): r.append(i + tmp) return r
The implementation above is very straightforward. The power of recursion is that you can split the problem into several subproblems and apply the exactly same machinery to each subproblem. This program simply takes the first element of each argument and concatenate it with every solution of this function with one fewer arguments (Fig 1).

So far we have seen functions which return all the results at a time. But in some applications such as searching or enumerating, you probably don't want to remember all combinations. What you want to do is just to inspect one combination at each time, and throw away after using it.
When the number of outputs is small, this is not a big deal. But what we expected for recursive procedures is to provide a quick solution for functions whose result grows exponentially, right? Ironically, however, such functions tend to produce a huge amount of data that cause problems in your program. In many language implementations, they cannot remember all the results. Sooner or later it will reach the maximum limit of the memory:
$ ulimit -v 5000 $ python ... >>> for x in fr(["abcdefghij","abcdefghij","abcdefghij","abcdefghij","abcdefghij"]): ... print x ... Traceback (most recent call last): File "<stdin>", line 1, in ? File "<stdin>", line 7, in fr MemoryError
The typical solution for this is to split every combination into different states. The typical way to do this in Python is to build an iterator.
In Python, a class which has a __iter__ method
can be used as iterators. Although iterators are not functionally
identical to lists, they can be taken instead of lists in some
statements or functions (for, map,
filter, etc).
class fi: def __init__(self, args): self.args = args self.counter = [ 0 for i in args ] self.carry = 0 return def __iter__(self): return self def next(self): if self.carry: raise StopIteration r = "".join([ arg1[i] for arg1,i in zip(self.args, self.counter) ]) self.carry = 1 x = range(len(self.args)) x.reverse() # x == [len(args)-1, len(args)-2, ..., 1, 0] for i in x: self.counter[i] += 1 if self.counter[i] < len(self.args[i]): self.carry = 0 break self.counter[i] = 0 return r # display def display(x): for i in x: print i, print return
In this program, you can use the constructor of the class
fi in the same manner as the recursive version fr as in:
>>> display(fi(["abc","def"]))
When this instance is passed to a for statement,
the __iter__ method is called and the returned object
(the object itself in this case) is used as the iterator of the
loop. At each iteration, the next method is called
without argument and the return value is stored in the loop
variable.
However, this program is not easy to understand.
Algorithmically, it is similar to the non-recursive version I
described above. Each time next method is called, it
updates the current state stored in counter variable
and returns one result according to the current state. But it
looks even more complicated, since the method is designed to be
called in between a loop, which is not shown explicitly here.
Readers might be upset by seeing that it checks carry
variable at the top of the next procedure. They have
to imagine an (invisible) loop outside this method to understand
this.
Note that this is not only simpler than the iterator version, but also even simpler than the original version with recursion. With generators, we can simply throw (or "yield") results one at a time, and forget them after that. It is just like printing results to a stream device. You don't have to really care about preserving states. All you have to do is just to produce all results recklessly, and still you can have strict control over that procedure. You might notice that the similar function can be realized withdef fg(args): if not args: yield "" return for i in args[0]: for tmp in fg(args[1:]): yield i + tmp return
lazy evaluation, which is supported in some functional languages. Although lazy evaluation and generators are not exactly same notion, both of them facilitate to handle the same situation in a different kind of form.
Perhaps functional programmers might prefer lambda encapsulation to objects. Python also allows us to do this. In fact, however, this was a real puzzle to me. I could do things in the same manner as I did the iterator version. But I wanted to do something different. After hours of struggles, I finally came up with something like this:
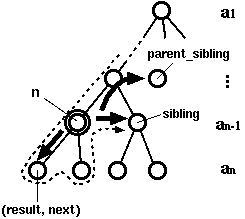
def fl(args, i=0, tmp="", parent_sibling=None): if not args: # at a leaf return (tmp, parent_sibling) if i < len(args[0]): # prepare my sibling sibling = fl(args, i+1, tmp, parent_sibling) return lambda: fl(args[1:], 0, tmp+args[0][i], sibling) else: # go up and visit the parent's sibling return parent_sibling # traverse function for lambda version def traverse(n): while n: if callable(n): # node n = n() else: # leaf (result, n) = n print result, print
The idea is indeed to take it as tree traversal. The function
f can be regarded as a tree which contains a partial result
at each node (Fig 2). A function produced by fl
retains its position, the next sibling node, and the next sibling
of the parent node in the tree. As it descends the tree, the
elements of the vectors are accumulated. When it reaches at a leaf
it should have one complete solution (a combination of elements).
If there is no node to traverse in the same level, it goes back to
the parent node and tries the next sibling of the parent node. We
need a special driver routine to traverse the tree.
Of course the generator version can be also regarded as tree traversal. In this case, you will be visiting a tree and dropping a result at each node.
CHANGES:
Jun 1, 2003: Released.
Jun 7, 2003: A small update based on the comments by Eli Collins.
Last Modified: Sat Jun 7 19:51:47 EDT 2003 (06/08, 08:51 JST)
Yusuke Shinyama